無料ダウンロード 数学 円周角 179854

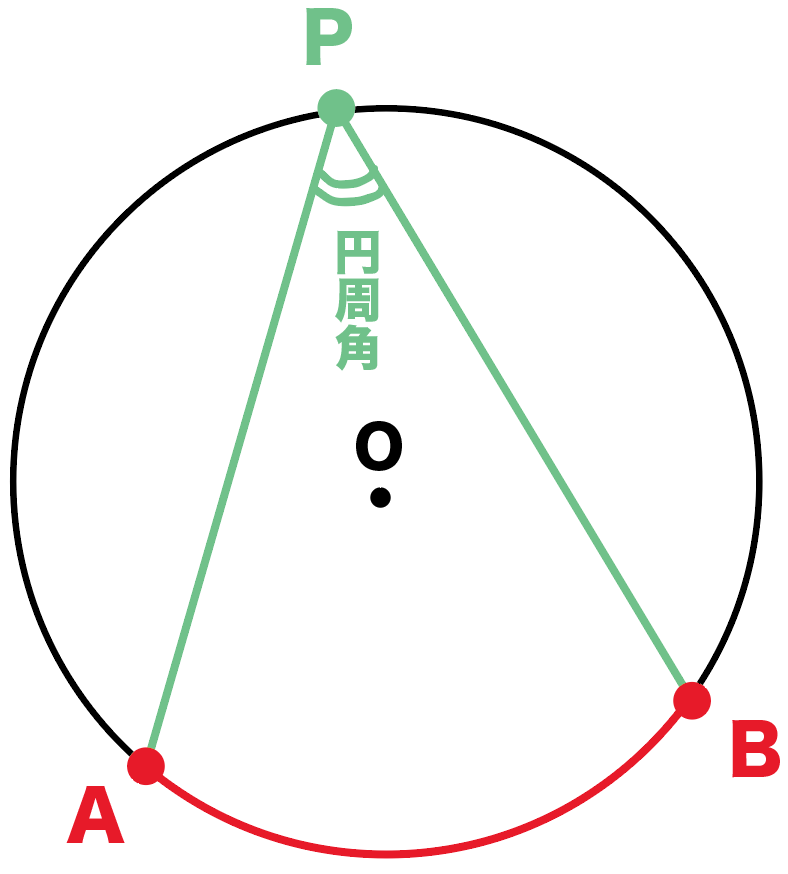
Studydoctor弧の長さと円周角の関係 中３数学 Studydoctor

岐阜数学教育研究 08, Vol7, 8794 円周角の定理の有用性を実感できる教材の開発 竹内洋平 1，愛木豊彦 生徒が日常の中に数学を発見することで，より数学を身近に感じ，数学を好きになれ るような教材の開発を試みた。 円周角や角度に関する問題は、難しい問題を作ろうと思えば作れますが、基本的にやることは同じであることが多いです。 まず、中心oの有無を確認するといいと思います。ここから色んなことがわかるからです。ひとつひとつ説明します。 円なので一番基本となるのは ①半径が等しい こ

数学 円周角

数学 円周角-円の性質 円周角と中心角・円周角の定理の逆 パワーポイント教材(228k) ワークシート1(円周角) ワークシート2（等しい弧に対する円周角） ワークシート3（円に内接する四角形） このプレゼンの動画はこちら 円の性質の利用 パワーポイント教材(173k) こんにちは！レオンです。 今回はこの問題を解いていこうと思います(*´ω`*) 19年の大阪教育大学附属高等学校平野校舎の過去問より。 円周角の定理を使った良い問題だと思います。 持っている知識を生かして柔軟に考えてみて下さい！ ヒント 答え 詳しい解説 ① 状況把握 ②

中３数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所

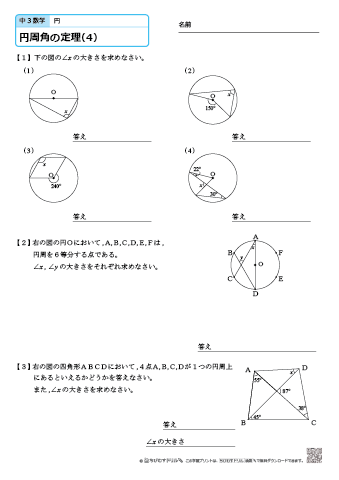
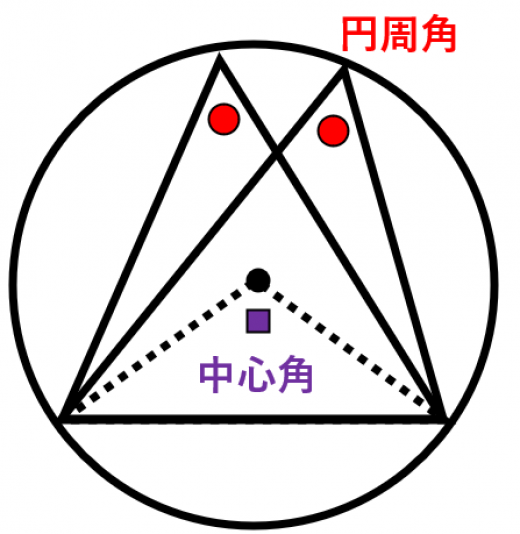
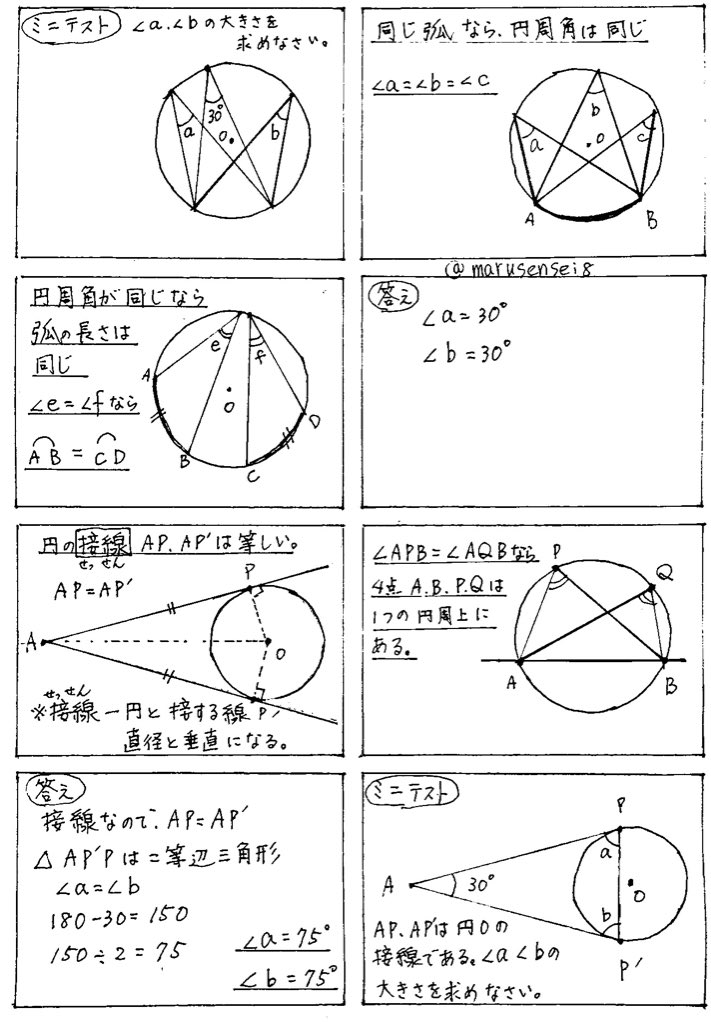
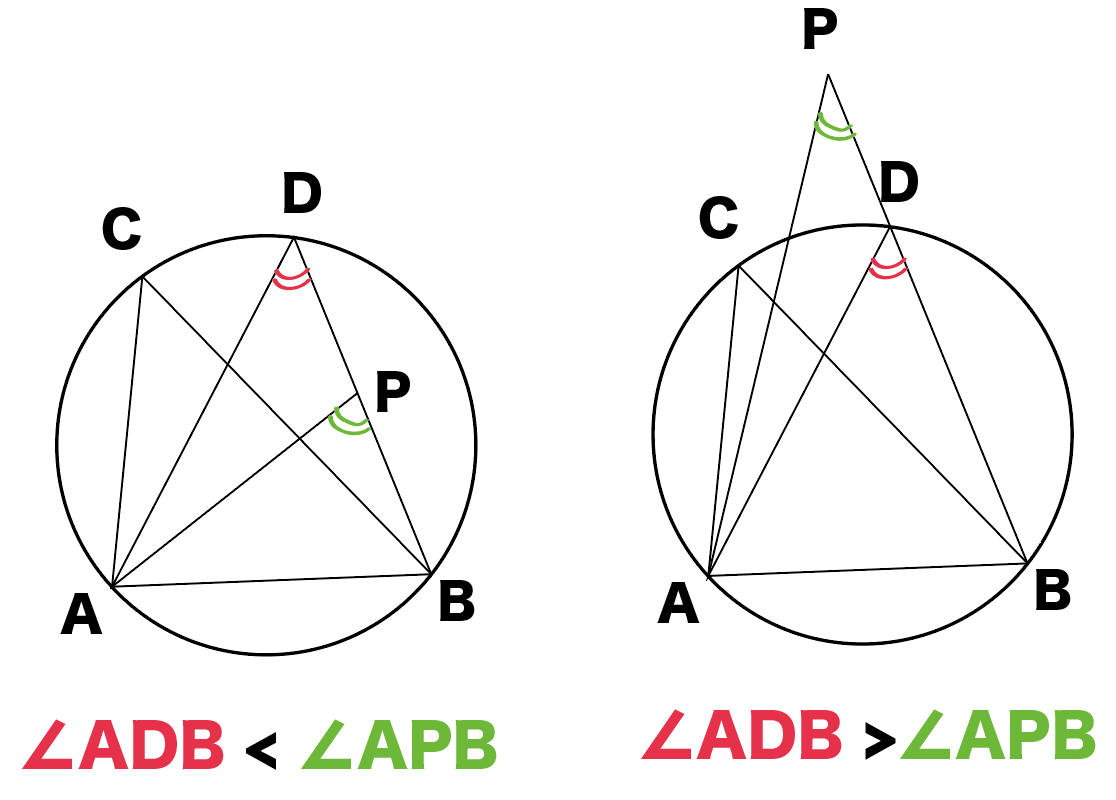
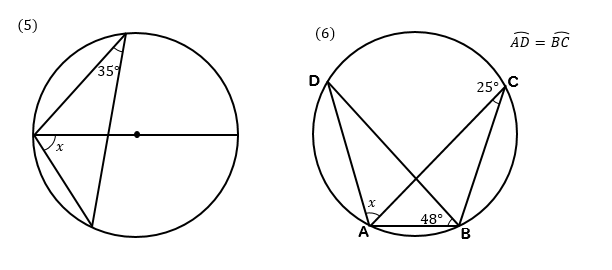
円周角の定理とは ①と②をあわせて、円周角の定理と言います。 ①は「同じ弧によって作られる円周角の大きさは、常に一定である」という意味です。 ∠ A P B = ∠ A P ′ B = ∠ A P ′ ′ B = 56 ° で一定であることが分かります。 次に、②は「円周角の円周角5(発展) 中学学習サイト 中学学習サイトは英語・数学・国語・理科・社会、中学5教科の無料練習問題を掲載しています。 練習問題は印刷してプリントとして使えるものから、pcやスマホから直接できるものまであり、普段の予習復習や定期テスト35分前 りりり 中3 数学 円周角の問題です。 xを求めよ。 という問題で、答えは28度らしいのですが解き方がわかりません>_< 解説お願いします🙇🏻‍♀️ 32° 円周角の定理

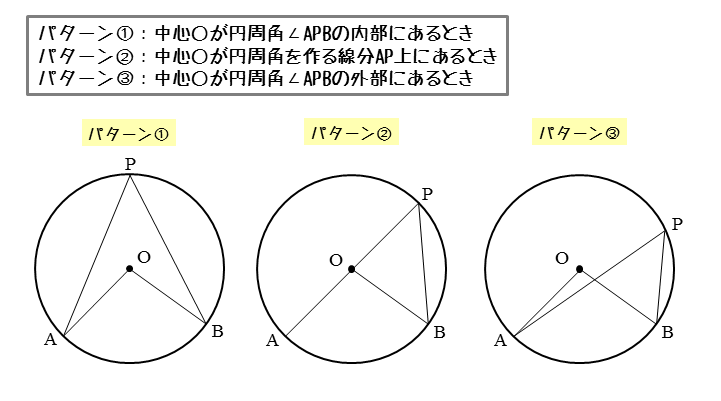
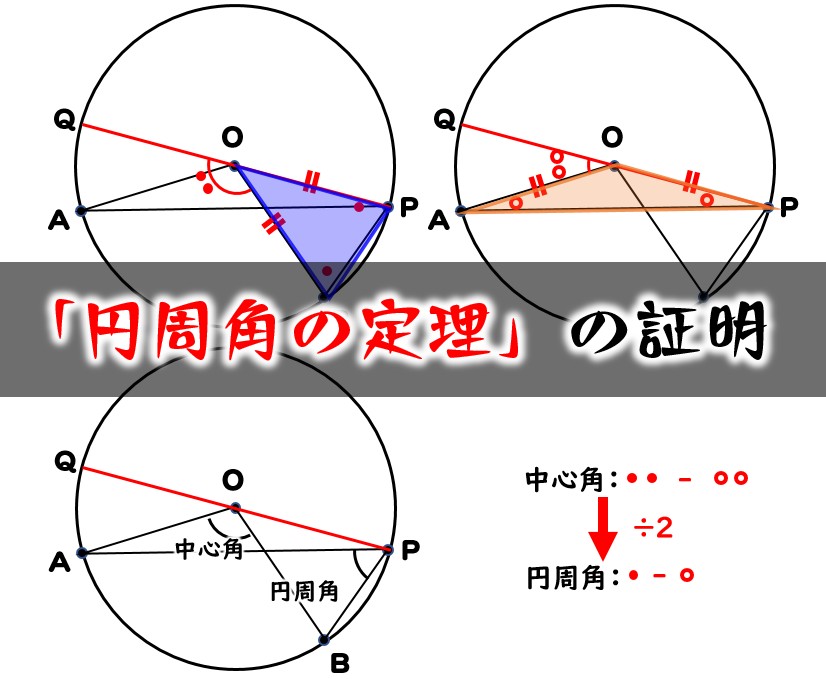
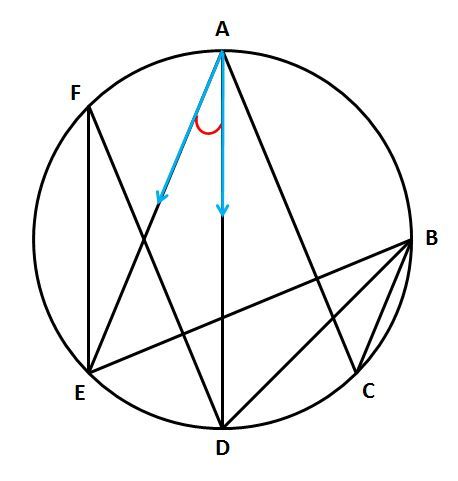
一般に，高校入試問題では「円周角の定理」を覚えているだけでは，問題は解けません．この問題では，次の2つの定理を組み合わせて解いています． (1) 一つの弧に対する円周角は等しい． (2) 三角形の内角の和は180°になる． 問題2 (1) 右の図のよう 今日の中3授業は 期末テスト対策＋入試対策も兼ねて 数学「相似比・円周角」を 念のため 総復習しておこう。 基礎基本から応用レベルまで 一気に 解法パターンをぶっ潰して 得点力をアップするよ 僕たちは どうせやるなら 数学こそ 100点満点💯 を狙いに行こうぜ 進プロ生なら 行けるよ円周角の定理は2つありますが、 「どんな場合でも円周角は常に中心角の半分である」 ということを示せば、両方の定理の証明になります。 より具体的に言えば、円周角をなす点Pの位置を動かして、3つのパターンにおいて常に円周角が中心角の半分である

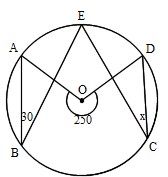
数学 円周角のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

円周角	円周角	円周角
円周角	円周角	円周角
円周角	円周角	円周角
円周角	円周角	円周角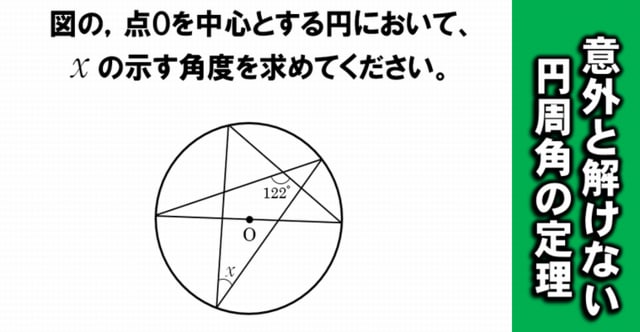
円周角	円周角	円周角
円周角	円周角	円周角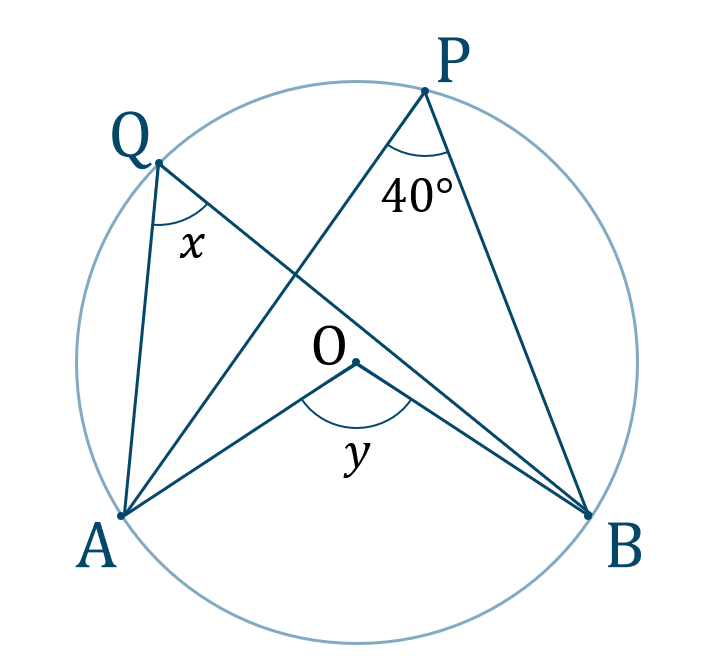
円周角	円周角	円周角
円周角	円周角	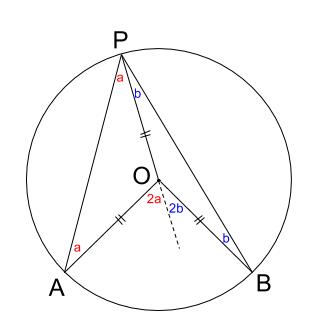円周角
円周角	円周角	円周角
円周角	円周角	円周角
円周角	円周角	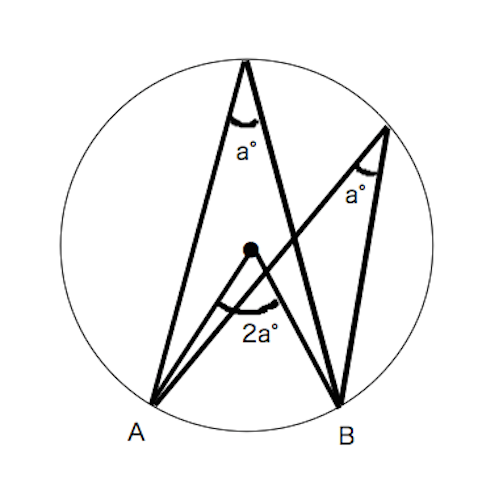円周角
円周角	円周角	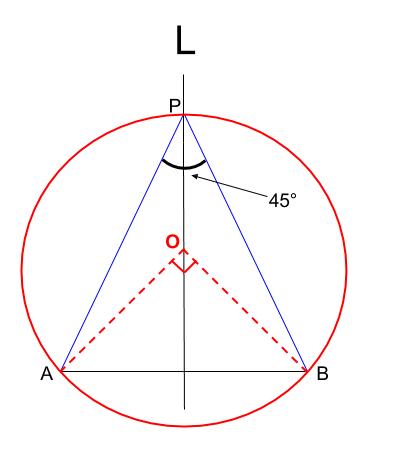円周角
円周角	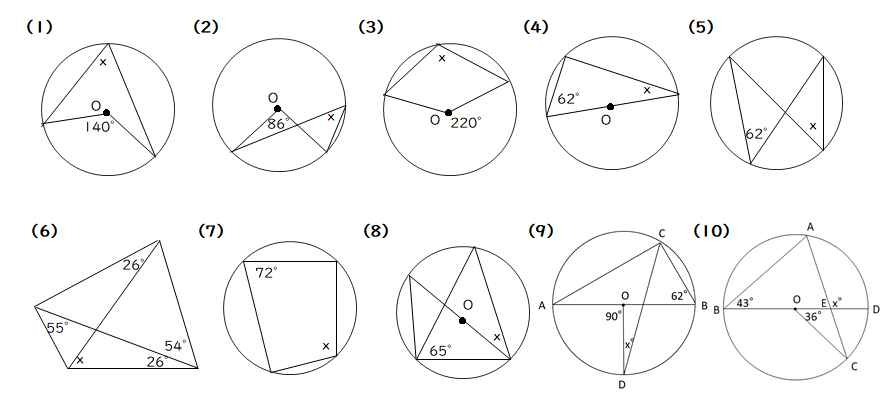円周角	円周角
円周角	円周角	円周角
円周角	円周角	円周角
円周角	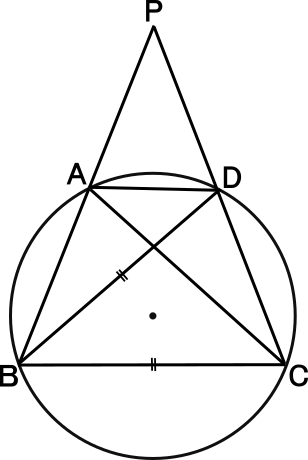円周角	円周角
円周角	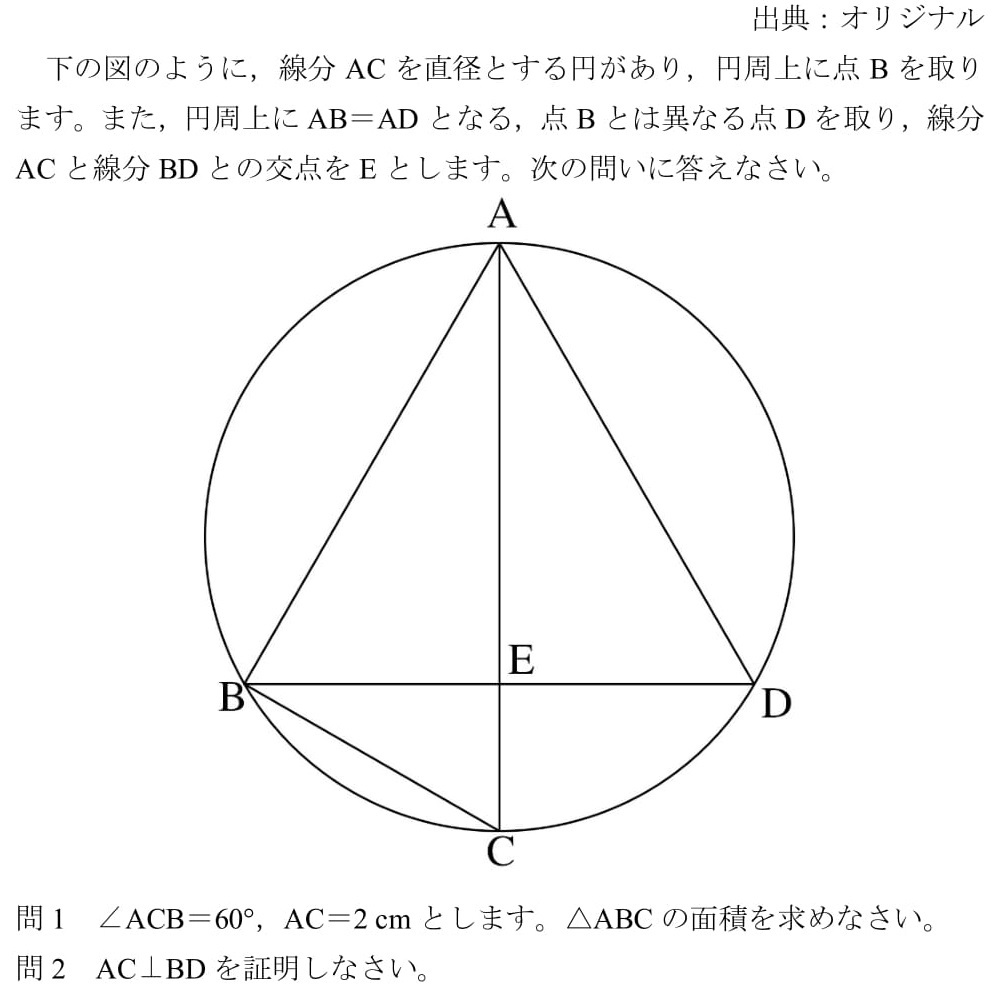円周角	円周角
円周角	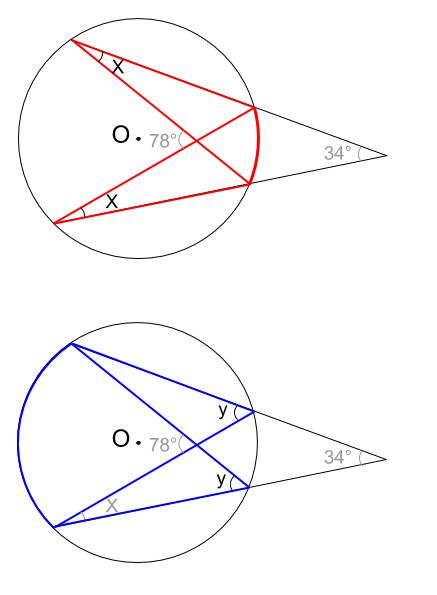円周角	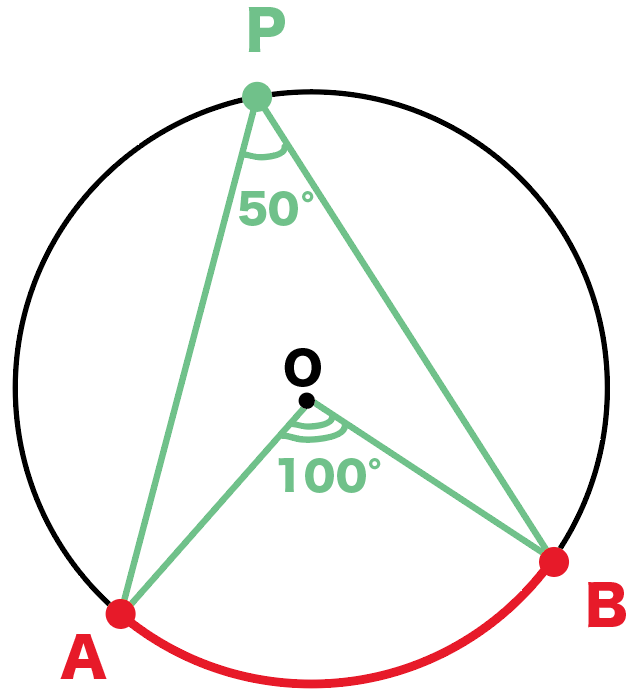円周角
円周角	円周角	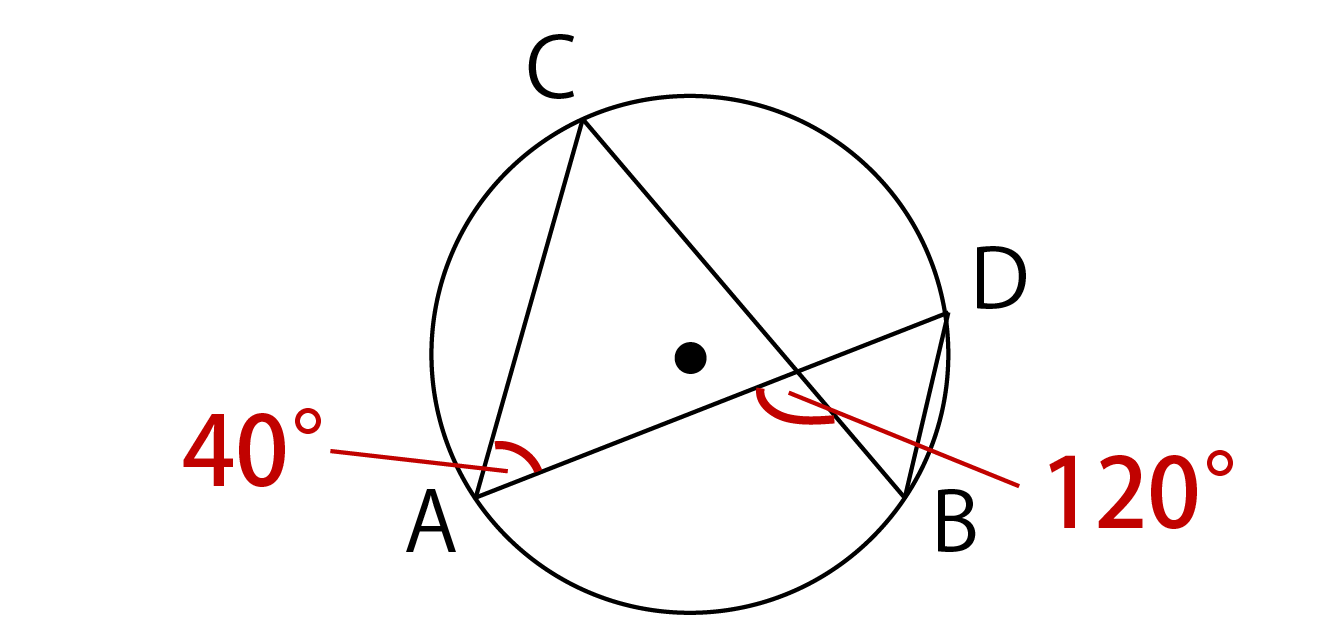円周角
円周角	円周角	円周角
円周角	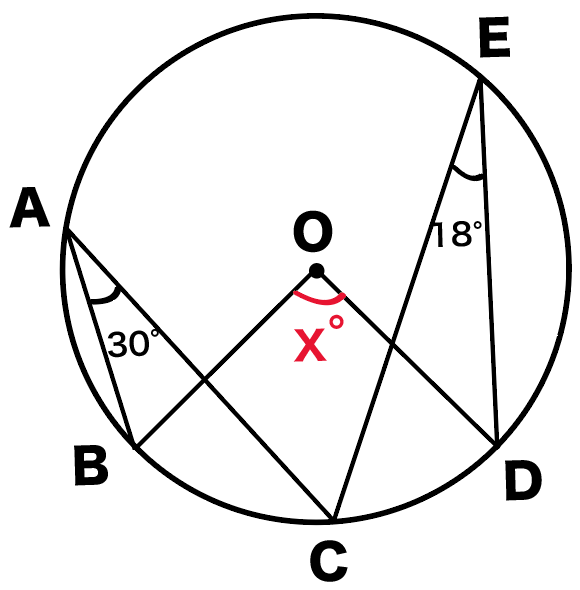円周角	円周角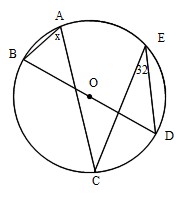
円周角	円周角	円周角
円周角	円周角	円周角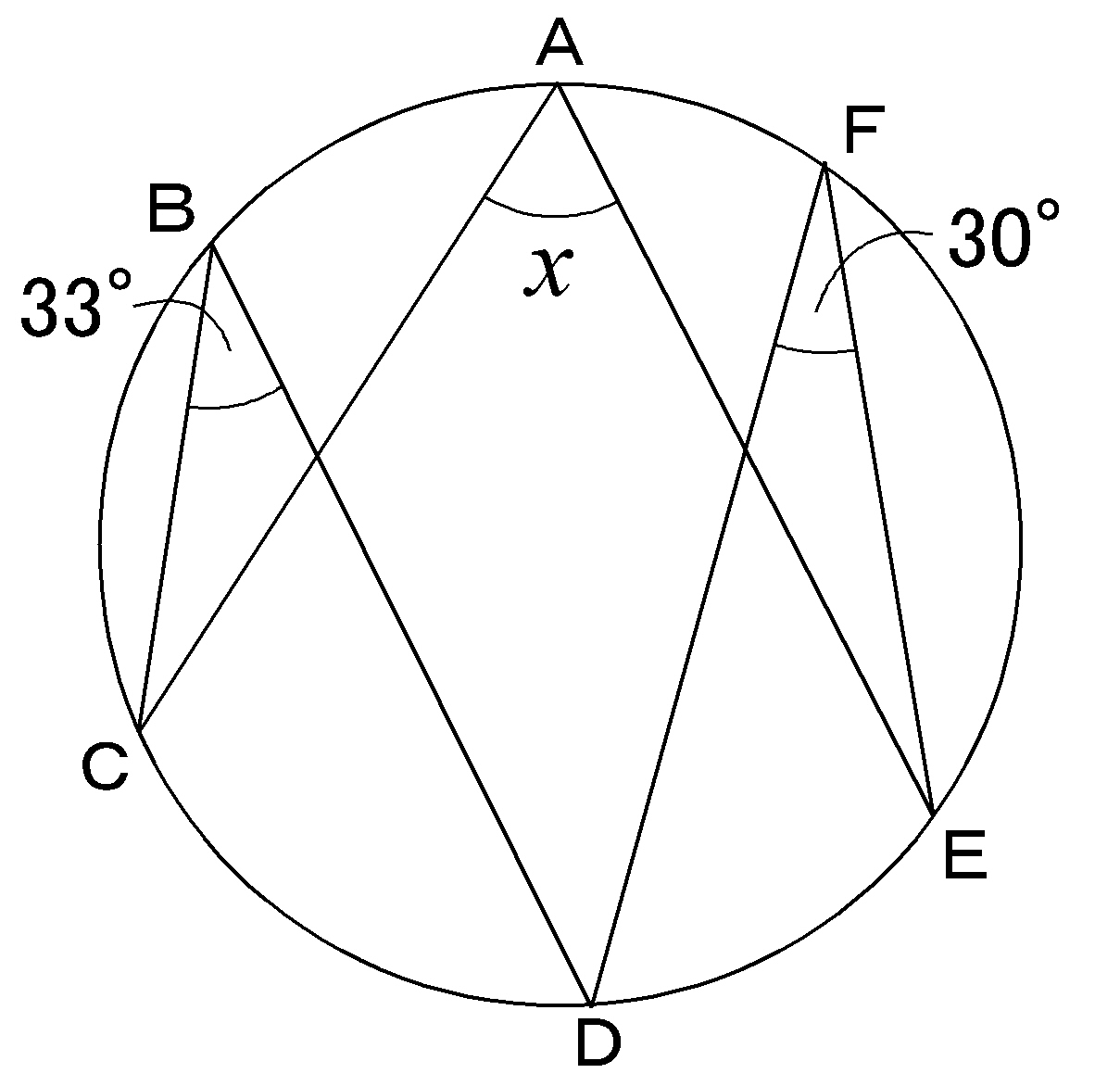
円周角	円周角	円周角
円周角	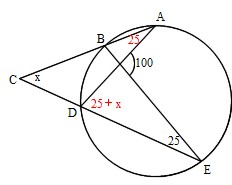円周角	円周角
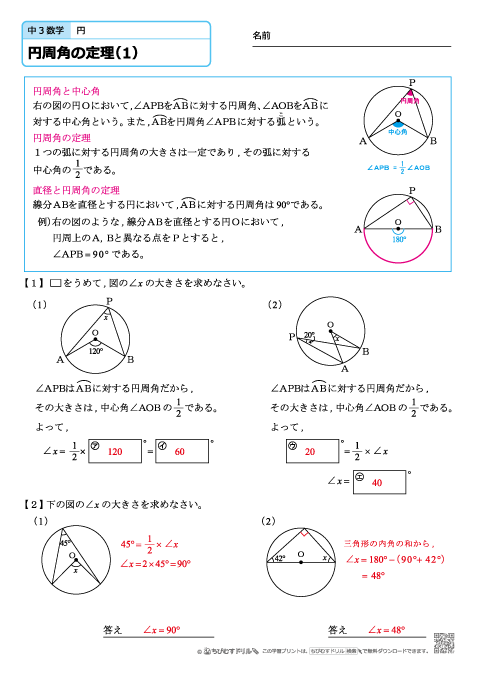円周角	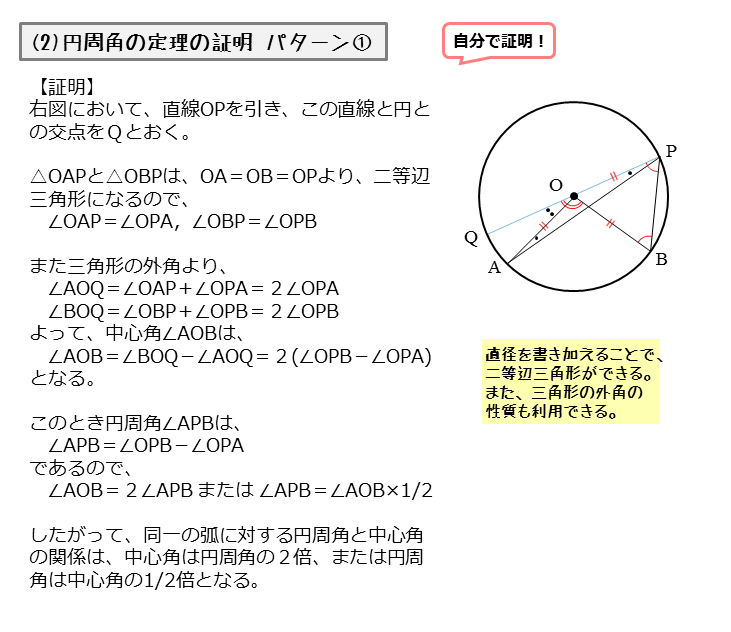円周角	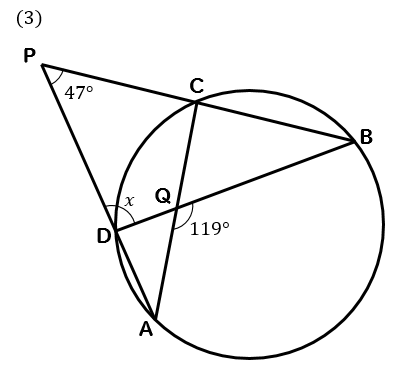円周角
円周角	円周角	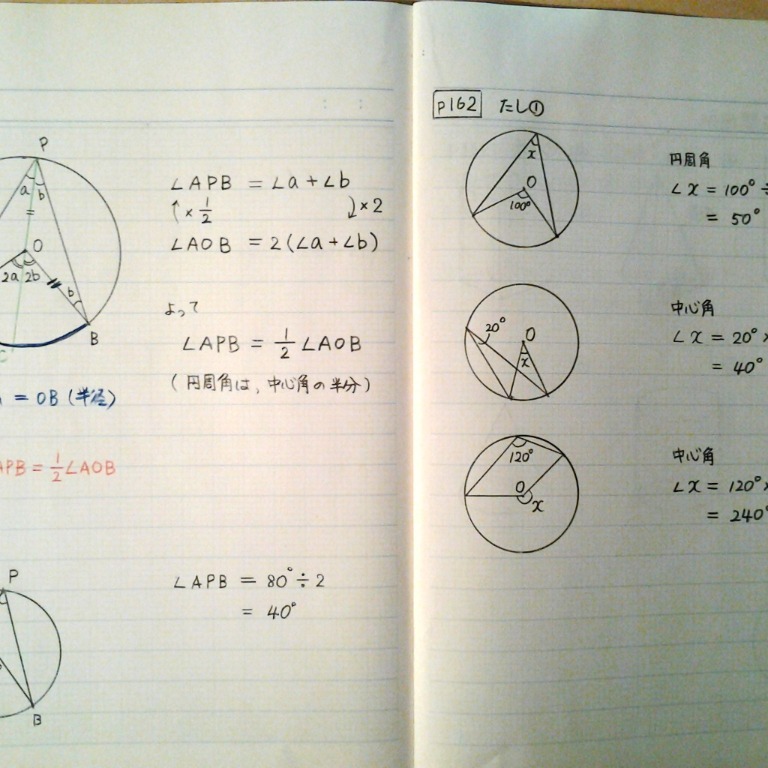円周角
円周角	円周角	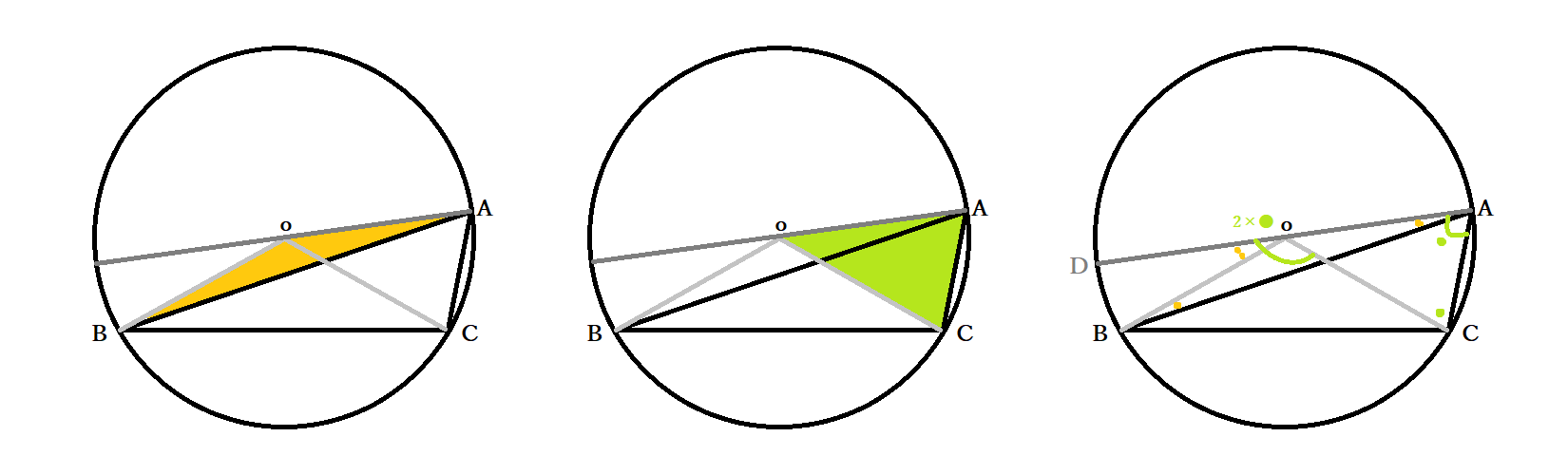円周角
円周角	円周角	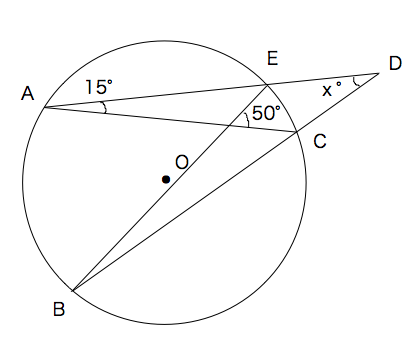円周角
円周角	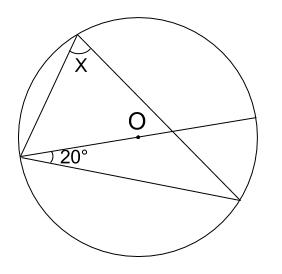円周角	円周角
円周角	円周角	円周角
円周角	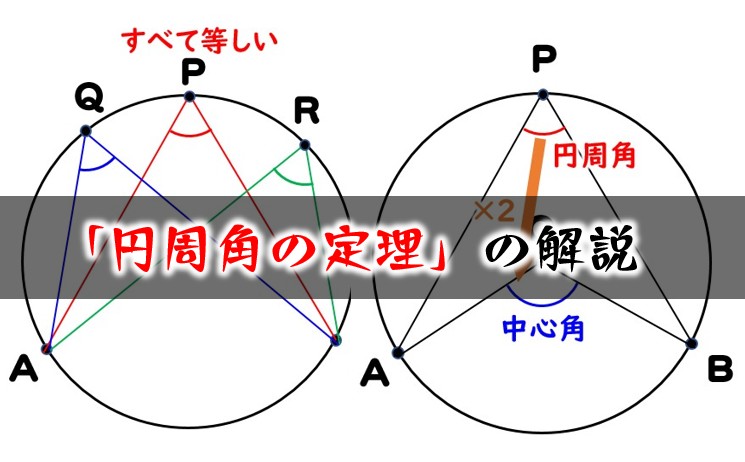円周角	円周角
円周角	円周角	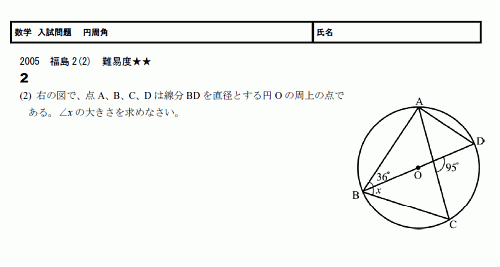円周角
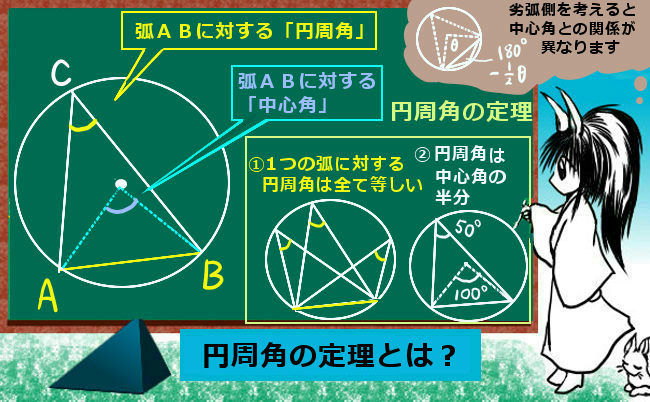円周角	円周角	円周角
円周角	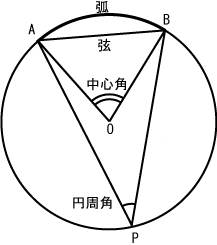円周角

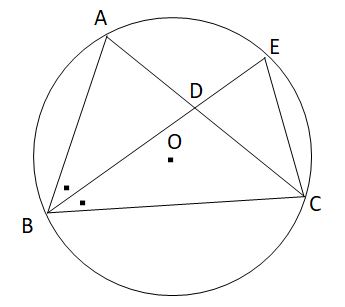
円周角1 円 円とは定点oから 一定の距離rにある点の集合 である。 このときの定点oを 円の中心 といい、距離rが 円の半径 である。 この定義を言い換えると、 「半径はどこでも等しい」 となる。 半径はどこでも等しいので、2つの半径oa, obと弦abによってできる三角形は必ず二等辺三角形である。第3学年 数学的な見方・考え方を養う「円周角の定理」の授業 ～動的幾何学ソフトウェア（GeoGebra）を用いて知識を拡張・統合する～ 岡山大学教育学部附属中学校 横林 慎也